Benvenuto nella rubrica How It Works!
Il concetto di entropia è utilizzato in molte aree della Data Science. L’entropia può essere utilizzata per sviluppare gli Alberi Decisionali (non hai mai sentito parlare degli Alberi Decisionali? Leggi il nostro articolo sull’argomento!), per quantificare la dipendenza di due variabili casuali (in un prossimo articolo si vedrà il concetto di “mutual information”) o ancora nell’ambito di procedure di “dimensionality reduction” come la t-SNE o la UMAP (ad entrambe le quali verrà presto dedicato un articolo, quindi resta sintonizzato!). In tutti i casi appena elencati, l’entropia è utilizzata come metrica per la quantificazione di similitudini e differenze.
Al fine di comprendere il significato dell’entropia nell’ambito della Data Science è prima necessario introdurre il concetto statistico di “sorpresa”. Si immagini di disporre di un cesto di frutta contenente 32 tra mele e arance e di suddividere i frutti nei seguenti tre insiemi:

Si intuisce facilmente come la probabilità di estrarre una mela sia alta attingendo dall’insieme A, bassa attingendo dall’insieme B e pari alla probabilità di estrarre un’arancia attingendo dall’insieme C. In altre parole, estrarre una mela lascerebbe sorpresi nel secondo caso, per nulla sorpresi nel primo e “mediamente sorpresi” nel terzo. Riflettendoci, si può affermare che, in qualche modo, il concetto di “sorpresa” sia inversamente proporzionale al concetto di “probabilità”.
Esiste un modo per calcolare la “sorpresa” relativa ad un evento probabilistico?
Essendo intuitivamente l’inverso della probabilità, si sarebbe tentati di calcolare la sorpresa semplicemente come segue:
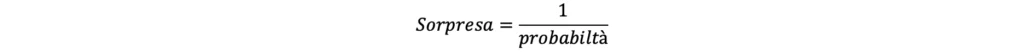
Questa equazione non si rivela tuttavia particolarmente efficace. S’immagini di lanciare una moneta truccata che restituisce sempre “testa”. Sapendo che la probabilità di ottenere “croce” è 0 (in quanto la moneta restituisce sempre irrimediabilmente “testa”), ci si aspetta un livello di sorpresa nullo associato all’evento “testa”. Considerando che la probabilità di ottenere “testa” in questo caso è pari ad 1, calcolando la sorpresa semplicemente utilizzando l’inverso della probabilità si otterrebbe tuttavia quanto segue:
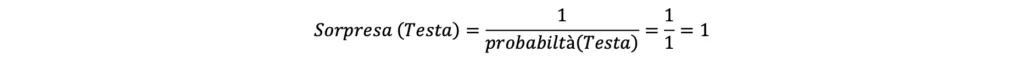
Nonostante ci si aspettasse un valore di sorpresa pari a 0 circa il risultato “testa”, calcolando la sorpresa semplicemente come inverso della probabilità di ottiene 1.
Una soluzione consiste nel calcolare la sorpresa come logaritmo dell’inverso della probabilità. Dunque:
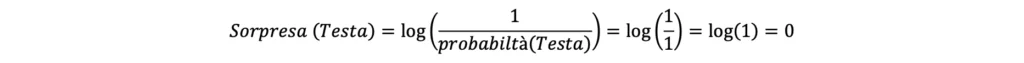
Tale equazione si dimostra coerente anche nel calcolo del valore di sorpresa associato all’evento “croce”, il quale in questo caso ha probabilità di accadimento pari a 0. Dunque:
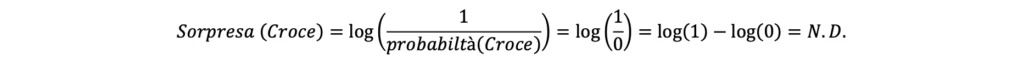
Il risultato N.D. (Non Definito) dovuto all’indefinitezza del logaritmo di 0 è coerente con il caso, in quanto non ha senso calcolare la sorpresa associata ad un risultato che non può avvenire (in quanto ha probabilità pari a 0). Tipicamente, quando si calcola la sorpresa legata ad un evento che può avere solamente due risultati (come appunto il lancio di una moneta) si utilizza il logaritmo in base 2 al posto del logaritmo naturale. L’equazione può essere quindi riscritta come segue:
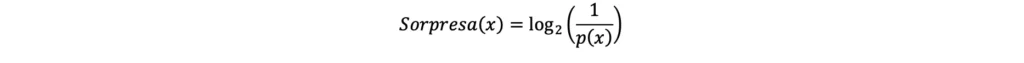
S’ipotizzi ora che il lancio della moneta abbia probabilità 0.9 di dare “testa” e 0.1 di dare “croce”. I valori di sorpresa associati ai due eventi “testa” e “croce” sono quindi i seguenti:
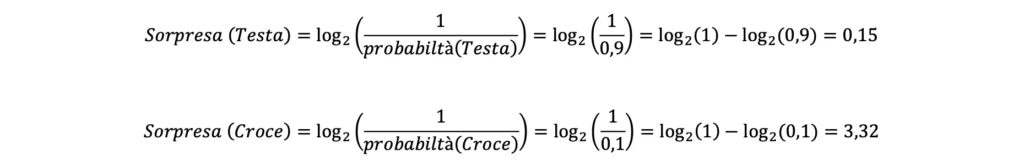
Immaginando di lanciare la moneta 3 volte, ottenendo come risultato “testa”, “testa” e “croce”, la probabilità di ottenere esattamente tale sequenza sarebbe la seguente:
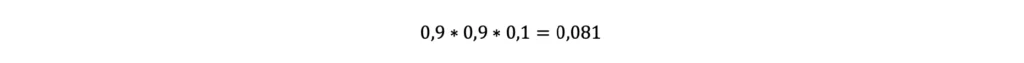
La sorpresa associata all’evento composto “testa”, “testa”, “croce” si calcolerebbe quindi come segue:
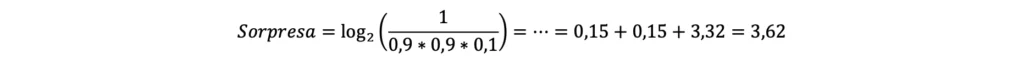
Si noti come la sorpresa relativa all’accadimento della sequenza “testa”, “testa”, “croce” sia pari alla somma dei valori di sorpresa relativi a ciascun singolo evento “testa” o “croce”. Il valore di sorpresa è quindi in un certo senso “cumulabile”. Supponendo ora di voler stimare il valore totale di sorpresa “accumulato” dopo 100 lanci della moneta, si procede come segue:
- Si stima il numero di volte, sui 100 lanci, nelle quali si otterrà “testa”:
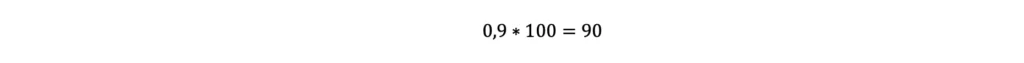
- Si stima il valore totale di sorpresa associato all’accadimento, 90 volte su 100 lanci, dell’evento “testa” moltiplicando 90 per il valore di sorpresa atteso dall’ottenimento di un singolo risultato “testa”, ovvero:
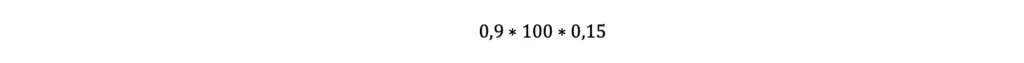
- Si stima il numero di volte, sui 100 lanci, nelle quali si otterrà “croce”:
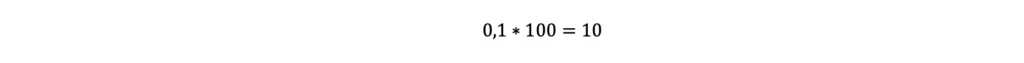
- Si stima il valore totale di sorpresa associato all’accadimento, 10 volte su 100 lanci, dell’evento “croce” moltiplicando 10 per il valore di sorpresa atteso dall’ottenimento di un singolo risultato “croce”, ovvero:

- Essendo la sorpresa cumulabile, si sommano le due stime dei valori di sorpresa, ottenendo una stima totale della sorpresa ottenuta dai 100 lanci della moneta. Dunque:

Dividendo la stima della sorpresa totale ottenuta dai 100 lanci per il numero di lanci (ovvero ancora per 100), si ottiene la “sorpresa media per singolo lancio della moneta”, anche detta “entropia” associata all’evento “lancio della moneta”. Dunque:
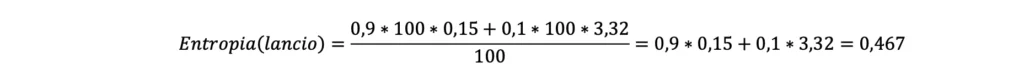
L’entropia legata ad un evento si definisce dunque come “il valore atteso della sorpresa legata a quell’evento”, ovvero, nella corretta notazione statistica:

Inserendo quindi nella formula sopra riportata la formula per il calcolo della sorpresa, si ottiene la definizione formale di entropia, ovvero:

Nonostante la formula dell’entropia appena riportata sia formalmente corretta, non è quella generalmente riportata sui libri di testo, sui quali si trova solitamente la seguente, del tutto equivalente (in quanto ricavata dalla precedente):
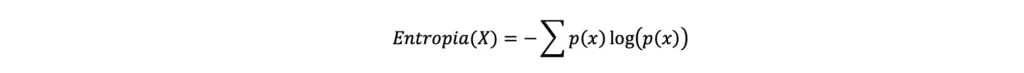
Quest’ultima formulazione, diventata per così dire “standard”, fu quella proposta da Claude Shannon nel 1948 nella sua pubblicazione dal nome “A Mathematical Theory of Communication”.

Ora, tornando all’esempio iniziale delle mele e delle arance, si può facilmente calcolare l’entropia relativa all’estrazione di un generico frutto da ciascun insieme (si utilizzerà di seguito, per semplicità, la prima formulazione di entropia introdotta precedentemente). Dunque:
- Insieme A: essendo presenti nell’insieme A 6 mele ed 1 arancia, si avrà quanto segue:
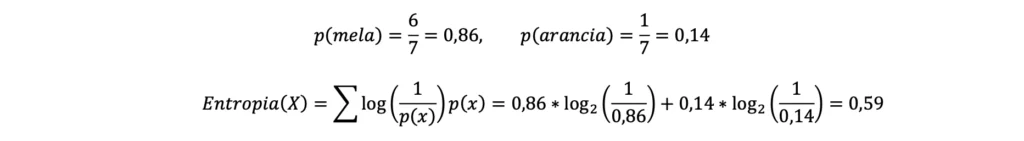
- Insieme B: essendo presenti nell’insieme B 1 mela e 10 arance, si avrà quando segue:
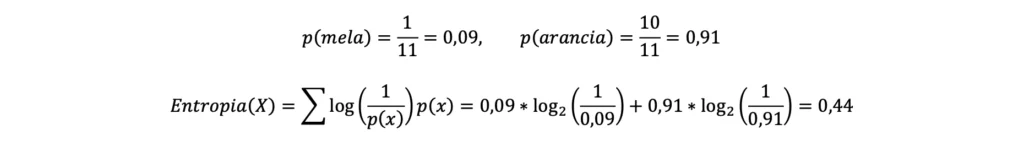
- Insieme C: essendo presenti nell’insieme C 7 mele e 7 arance, si avrà quanto segue:
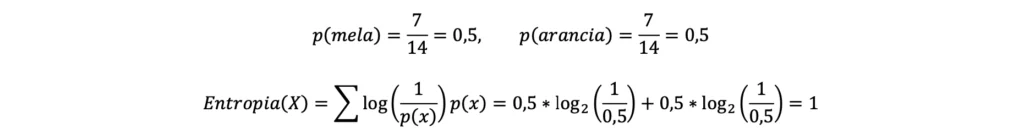
L’entropia è utilizzata nell’esempio per quantificare il divario (o, volendo, la “somiglianza” o la “differenza”) tra il numero di mele e arance all’interno di ciascun gruppo ed è quindi alta nell’insieme C, dove non c’è una prevalenza di mele o arance, per diminuire poi mano a mano che aumenta la differenza tra il numero di mele e arance, come si può vedere dai risultati associati agli insiemi A e B.
Applicando il concetto di entropia alle funzioni di probabilità, una funzione di distribuzione di probabilità avrà quindi un valore di entropia tanto più alto quanto più avrà valori di probabilità uniformi (ovvero uguali tra loro) per tutti i valori della variabile casuale X. Ovvero:
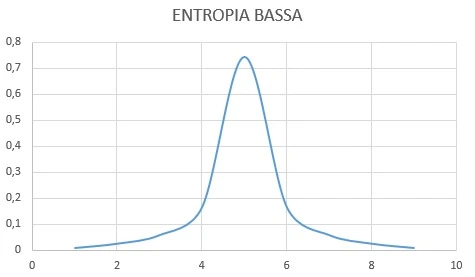
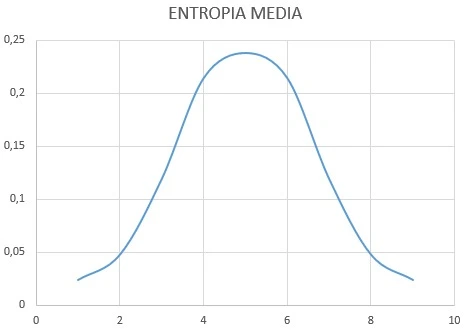
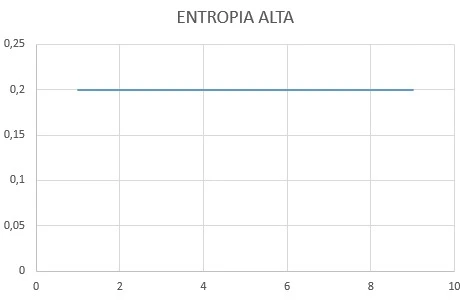
Come si può vedere dall’immagine, l’entropia è bassa per la funzione di distribuzione di probabilità altamente concentrata su uno specifico valore, è media per la funzione di distribuzione di probabilità meno concentrata e alta per la funzione di distribuzione di probabilità rettilinea uniforme. Ricollegandosi all’esempio del cesto di frutta, l’entropia sarebbe quindi bassa in un cesto contenente moltissime arance, poche mele e pochi elementi di altri frutti, un po’ più alta in un cesto contenente molte arance e un numero minore ma comparabile di mele ed altri frutti ed alta in un cesto contenente un’uguale quantità di ciascun frutto.
Si può quindi affermare, con un certa “licenza poetica”, che l’entropia di una funzione di distribuzione di probabilità misuri il “livello di disordine” di tale funzione, nel senso della propensione della variabile casuale ad assumere valori diversi con probabilità simile.
Francesco
