Benvenuto nella rubrica How It Works!
Gli alberi decisionali sono modelli di Machine Learning supervisionato che implementano una strategia molto diversa rispetto ad altri modelli della stessa categoria, come ad esempio le reti neurali. Sono chiamati “alberi” perché la loro struttura assomiglia ad un albero capovolto: partendo da un “nodo radice”, l’albero si ramifica progressivamente fino ad arrivare alle foglie.
Come per altri algoritmi supervisionati, ad esempio le reti neurali, gli alberi decisionali sono costruiti per estrarre conoscenza da un insieme di dati e renderla utilizzabile per eseguire una previsione. Una volta allenato il modello su un insieme di dati etichettati, questo sarà in grado di fornire una risposta circa il valore di una determinata variabile target associata ad una nuova osservazione (che non era presente nei dati utilizzati per l’addestramento).
Si consideri ora il seguente semplice esempio, nel quale il dataset riportato viene utilizzato per addestrare un albero decisionale al fine di ottenere un modello in grado di restituire previsioni sul prezzo delle abitazioni di una specifica città. Dunque:

Le variabili “Località”, “Dimensione”, “Numero di stanze”, “Numero di bagni”, “Anno di costruzione” e “Tipo di proprietà” contengono tutti i dati sui quali il modello viene allenato per prevedere il prezzo dell’abitazione, quest’ultimo contenuto nella variabile “Prezzo” (anche detta “etichetta” o “variabile target”).
Ogni nodo dell’albero rappresenta una variabile e ogni ramo rappresenta una “decisione” (anche detta “regola”) basata su quella variabile. Le foglie dell’albero rappresentano le previsioni. Di seguito si analizza nel dettaglio come un albero decisionale potrebbe essere utilizzato per prevedere il prezzo delle case utilizzando il dataset sopra riportato. Dunque:
Scelta della variabile di divisione: l’algoritmo inizia scegliendo (sulla base del calcolo di determinate metriche che qui non verranno approfondite) la variabile che meglio separa i dati in base alla variabile target (ovvero in base al prezzo).
Divisione dei dati: partendo dunque dal nodo radice, si suddividono le osservazioni dell’intero dataset in due o più sottoinsiemi basati sulla variabile scelta.
Ripetizione del processo: il processo di scelta della variabile di suddivisione si ripete per ogni sottoinsieme, creando ulteriori nodi e rami, fino a quando non vengono soddisfatti determinati criteri di arresto dell’algoritmo (ad esempio, un numero minimo di osservazioni per foglia o una profondità massima dell’albero).
Previsione tramite l’albero allenato: per effettuare una previsione, una nuova osservazione (nell’esempio, una nuova casa con le relative caratteristiche descritte dalle sue variabili) viene introdotta in input nell’albero decisionale. Sulla base dei valori delle variabili dell’osservazione di input, si percorreranno le ramificazioni dell’albero fino ad arrivare ad una determinata estremità, ovvero ad una determinata foglia. A tale estremità corrisponderà un campione delle osservazioni contenute nel dataset utilizzato per il training (nell’esempio corrente, un insieme di case, ciascuna con il proprio prezzo). La previsione in merito alla nuova osservazione viene quindi ottenuta tramite il calcolo di una specifica statistica (come ad esempio la media aritmetica) che riassuma i valori della variabile target relativi alle osservazioni contenute nella foglia.
Di seguito si analizza quindi nel dettaglio come avverebbe la suddivisione durante la fase di training di un albero decisionale sul semplice dataset dell’esempio riportato sopra. Dunque:
Nodo Radice: si supponga che l’algoritmo inizi la suddivisione tramite la variabile “Dimensione”. La soglia scelta potrebbe essere, ad esempio, 100 mq. Dunque:
Se Dimensione (mq) <= 100 l’osservazione del dataset viene inserita nel sottogruppo di sinistra.
Se Dimensione (mq) > 100 l’osservazione del dataset viene inserita nel sottogruppo di destra.
Primo livello di suddivisione:
Sinistra (Dimensione <= 100):
Ulteriore suddivisione basata sulla variabile “Località”.
Se “Località” = “Centro città” l’osservazione del dataset viene inserita nel sottogruppo di sinistra.
Se “Località” = “Periferia” l’osservazione del dataset viene inserita nel sottogruppo di destra.
Destra (Dimensione > 100):
Ulteriore suddivisione basata sulla variabile “Numero di stanze”.
Se “Numero di stanze” >= 3 l’osservazione del dataset viene inserita nel sottogruppo di sinistra.
Se “Numero di stanze” < 3 l’osservazione del dataset viene inserita nel sottogruppo di destra.
Fino ad ora, l’albero avrà quindi la seguente struttura. Dunque:
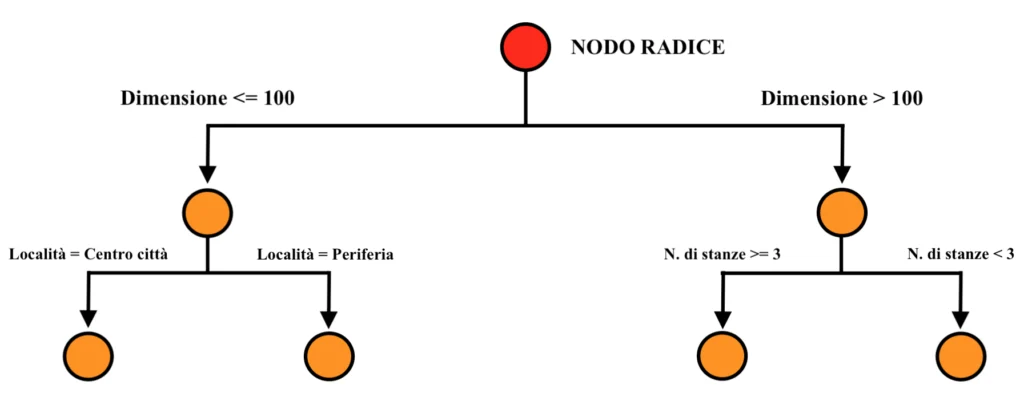
Secondo livello di suddivisione:
Sinistra sottogruppo 1 (Dimensione <= 100 e Località = Centro città):
Se “Numero di bagni” >= 2 l’osservazione del dataset viene inserita nel sottogruppo di sinistra.
Se “Numero di bagni” < 2 l’osservazione del dataset viene inserita nel sottogruppo di destra.
Sinistra sottogruppo 2 (Dimensione <= 100 e Località = Periferia):
Se “Tipo di proprietà” = Villa l’osservazione del dataset viene inserita nel sottogruppo di sinistra.
Se “Tipo di proprietà” = Casa a schiera l’osservazione del dataset viene inserita nel sottogruppo centrale.
Se “Tipo di proprietà” = Appartamento l’osservazione del dataset viene inserita nel sottogruppo di destra.
Destra sottogruppo 1 (Dimensione > 100 e Numero di stanze < 3):
Se “Anno di costruzione” >= 2000 l’osservazione viene inserita nel sottogruppo di sinistra.
Se “Anno di costruzione” < 2000 l’osservazione viene inserita nel sottogruppo di destra.
Destra sottogruppo 2 (Dimensione > 100 e Numero di stanze >= 3):
Se “Tipo di proprietà”= Villa l’osservazione viene inserita nel sottogruppo di sinistra.
Se “Tipo di proprietà” = Appartamento l’osservazione viene inserita nel sottogruppo centrale.
Se “Tipo di proprietà” = Casa a schiera l’osservazione viene inserita nel sottogruppo di destra.
Una volta completato l’addestramento, l’albero in questione sarà quindi il seguente. Dunque:
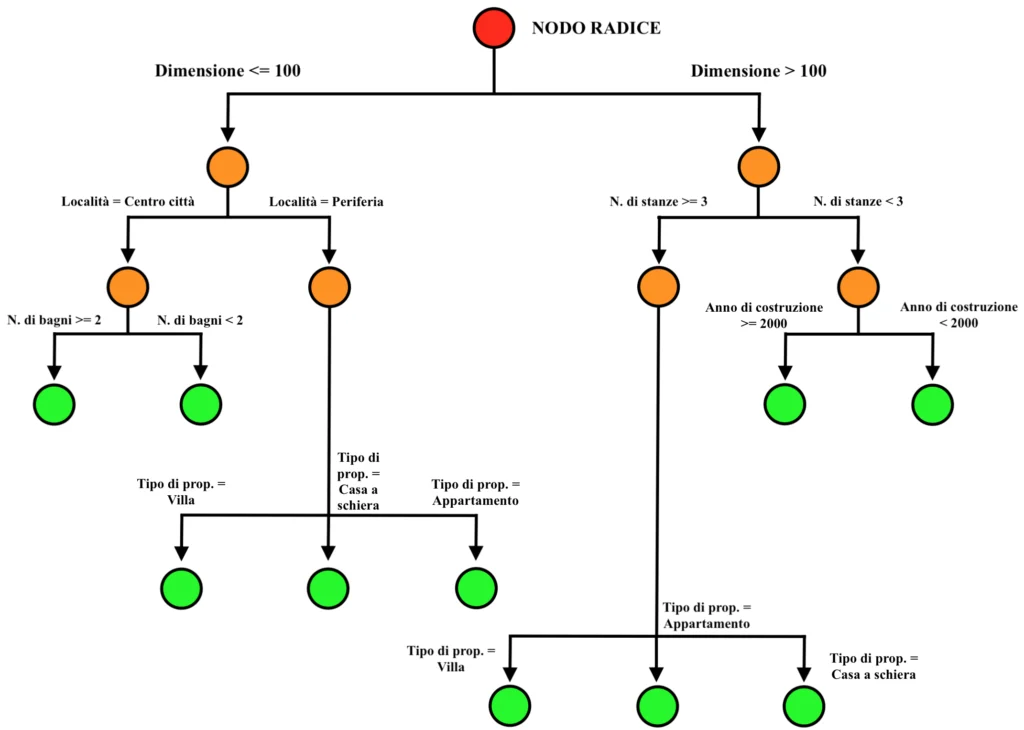
Si supponga ora che, disponendo della capacità previsionale dell’albero decisionale addestrato, si voglia eseguire una previsione circa il prezzo di una casa avente le seguenti caratteristiche. Dunque:
- Località = Periferia
- Dimensione = 130 mq
- Numero di stanze = 4
- Numero di bagni = 2
- Anno di costruzione = 2010
- Tipo di proprietà = Villa
Partendo dal nodo radice, essendo il valore della variabile “Dimensione” maggiore di 100, si imbocca il ramo di destra.
Giunti quindi al primo livello dell’albero, essendo il valore della variabile “Numero di stanze” maggiore di 3, si imbocca il ramo di sinistra.
Giunti al secondo livello dell’albero, essendo l’anno di costruzione maggiore di 2000, si imbocca il ramo di sinistra.
Non essendo presenti ulteriori suddivisioni in sottogruppi, si è quindi giunti ad una delle foglie dell’albero.
La foglia è quindi un sottogruppo terminale di elementi, il quale non viene più ramificato in ulteriori sottogruppi, e la previsione è così fornita dal calcolo di una qualche statistica arbitraria che riassuma il valore della variabile target relativo agli elementi contenuti nella foglia.
Una classica e semplice statistica descrittiva utilizzata nei problemi di regressione (come quello corrente, si vuole infatti prevedere il prezzo di una casa, il quale è un valore numerico continuo) è la media aritmetica.
La previsione di prezzo associata alla nuova osservazione sarà così pari alla media dei prezzi delle osservazioni del dataset di training che sono state inserite nel sottogruppo (alla foglia) al quale si è arrivati seguendo i valori delle variabili dell’osservazione stessa.
Gli alberi decisionali sono quindi un modello (cosiddetto “non parametrico”, in quanto durante il training non vengono ottimizzati i parametri di una funzione matematica per effettuare le previsioni; in questo senso, come accennato inizialmente, gli alberi decisionali sono radicalmente diversi da altri modelli “parametrici” di apprendimento supervisionato, come ad esempio le reti neurali) in grado di costruire una “mappa” del dataset di training, il quale viene suddiviso in tanti (per applicazioni complesse si parla di milioni) sottogruppi, e di utilizzare questa mappatura per ricondurre i nuovi esempi (non presenti nel dataset di training) in uno di questi sottogruppi al fine di ricavare un valore previsionale.
Sebbene le potenzialità di questi modelli possano intuitivamente sembrare molto grandi, tali modelli tendono a soffrire particolarmente di un classico e spesso letale problema che affligge i modelli di Machine Learning: il cosiddetto “sovradattamento” (in inglese, “overfitting”). Un modello “sovradattato” ha “imparato troppo bene” le caratteristiche del training set e si trova completamente o quasi incapace di generalizzare le conoscenze apprese per effettuare una previsione utile su dati nuovi. Più è lasciata libertà all’albero decisionale di approfondire la suddivisione del dataset di training in sottogruppi sempre più specifici e maggiore sarà il rischio di overfitting. Approfondiremo questo problema in un articolo interamente dedicato al sovradattamento!
Un grande punto a favore degli alberi decisionali è invece la cosiddetta “explainability”, ovvero la possibilità, per un analista umano, di comprendere i “ragionamenti” effettuati dal modello (insomma, il perché ha espresso proprio quella previsione di prezzo per una casa con quelle caratteristiche). Mentre per una rete neurale, per questo detta “modello black box”, è sostanzialmente impossibile comprendere le esatte ragioni per le quali è stata espressa una determinata previsione (in quanto la funzione elaborata durante il training è, nelle applicazioni reali, sempre troppo complessa), utilizzando un albero decisionale si potrà sempre (anche se spesso potrebbe comunque essere molto difficile) ripercorrere le ramificazioni create dal modello per comprendere le ragioni che hanno portato all’output previsionale.
