Benvenuto nella rubrica How It Works!
In questo articolo analizzeremo il funzionamento di uno tra i più famosi modelli di machine learning non supervisionato: il famigerato K-Means!
Come già approfondito nel nostro precedente articolo riguardante le tre macro-aree di ricerca del machine learning, l’apprendimento non supervisionato è la branca che, semplificando, produce modelli matematici in grado di raggruppare i dati in base alla “somiglianza reciproca”. La domanda sorge spontanea: come si stabilisce se due record di un generico dataset sono tra loro “simili”?
Consideriamo la seguente tabella, contenente dati numerici relativi ad un gruppo di persone e riguardanti le seguenti caratteristiche. Dunque:
- Età
- Peso
- Altezza
- Genere
- Reddito annuo lordo
- Colore di capelli (1 per “capelli chiari”, 0 per “capelli scuri”)
- Numero di volte in cui hanno mangiato polenta e spezzatino nel 2023
- Numero di partite di campionato del Napoli seguite nel 2023
- Area italiana di residenza (si suddivide l’Italia in nord e sud, rispettivamente 1 e 0).
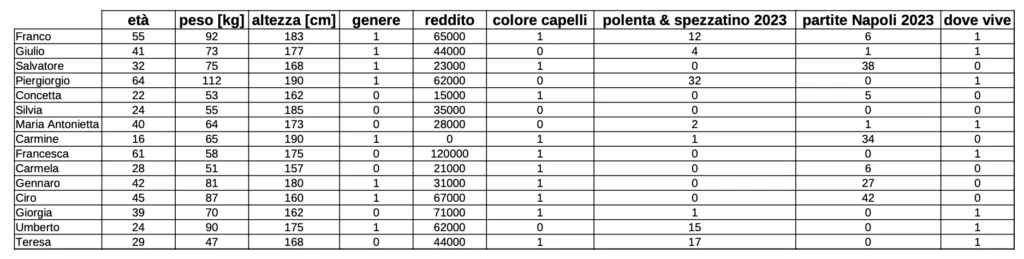
Analizziamo il primo record. Dunque:
Franco: 55, 92, 183, 1, 65000, 1, 12, 6, 1
Ciascuna colonna della tabella contiene una variabile numerica che fornisce un’informazione specifica su una caratteristica della persona alla quale è riferita, in questo caso un’informazione riguardante Franco.
Come si può facilmente intuire, tra le variabili è presente una più o meno forte correlazione; ad esempio, è decisamente probabile che Piergiorgio, che nel 2023 ha mangiato 32 volte polenta e spezzatino e che non ha visto nemmeno una partita del Napoli, viva da qualche parte nel nord Italia. È altrettanto probabile che Salvatore, il quale alla polenta preferisce di gran lunga i paccheri con il sugo di pesce e che durante il 2023 non ha perso una singola partita di campionato del Napoli, viva da qualche parte nel sud Italia. Le variabili “polenta & spezzatino 2023”, “partite Napoli 2023” e “dove vive” presentano quindi verosimilmente un’importante correlazione reciproca ed è proprio su tali correlazioni che uno tra i più utilizzati modelli matematici di apprendimento non supervisionato, il K – Means, basa le sue “considerazioni” per determinare se due record di un dataset vadano o meno inseriti nello stesso gruppo o, come si dice in gergo, nello stesso “cluster”.
Ciascun record individua uno specifico punto in uno spazio caratterizzato da tante dimensioni quante sono le variabili che lo descrivono. Ad esempio, se Franco fosse descritto solamente tramite l’età, l’altezza e il reddito, il record individuerebbe uno specifico punto in uno spazio tridimensionale, facilmente rappresentabile su un foglio di carta e del tutto simile al seguente. Dunque:
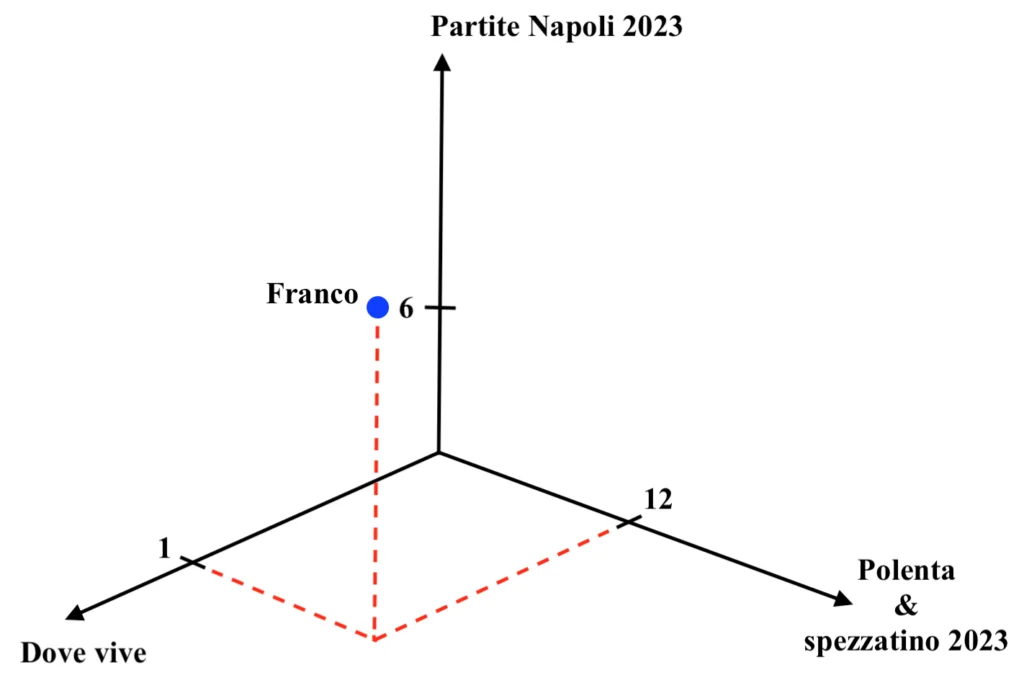
Essendo in questo caso le variabili 9, ciascun record individuerà un punto in uno spazio a 9 dimensioni, ovviamente non rappresentabile su carta bensì solo numericamente. Ma quindi come si determina se due record, ad esempio Franco e Salvatore, sono simili tra loro?
La “somiglianza” tra due record è misurabile come la distanza (nel senso più comune del termine) all’interno dello spazio descritto dalle variabili. Due record sono quindi tanto più simili quanto più si trovano vicini all’interno dello spazio nel quale sono individuati.
L’obiettivo del K-Means è quindi duplice: massimizzare la similarità intra-cluster e minimizzare la similarità inter-cluster. Tradotto in parole semplici, l’obiettivo è suddividere i record in gruppi in modo che gli elementi inseriti in ciascun gruppo siano allo stesso tempo il più possibile simili tra loro ed il più possibile diversi da quelli inseriti in tutti gli altri gruppi.
Tramite l’approccio K – Means, una volta prestabiliti dallo sviluppatore il numero di cluster secondo i quali si vogliono suddividere i record presenti all’interno del dataset, si esegue iterativamente la seguente procedura. Dunque:
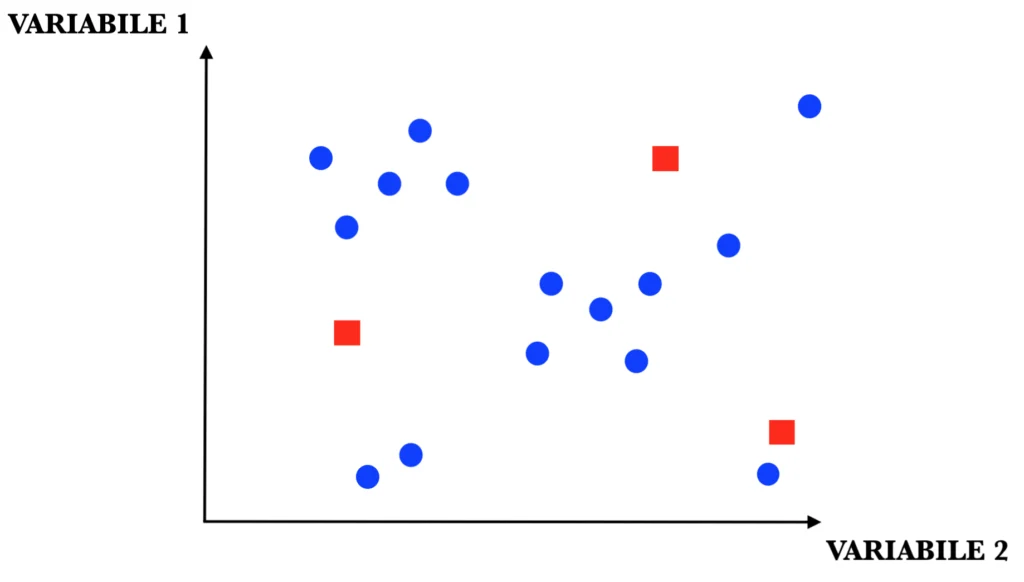
STEP 1: inizializzazione dei “centroidi”. I centroidi sono il “cuore” di ciascun cluster e sono utilizzati per determinare se un record appartiene o meno al gruppo in questione. Tale inizializzazione può essere casuale o avvenire secondo svariaticriteri statistici.
STEP 2: definizione dell’appartenenza di ogni record ad uno specifico cluster. Molto semplicemente, ogni elemento del dataset è assegnato al centroide più vicino.
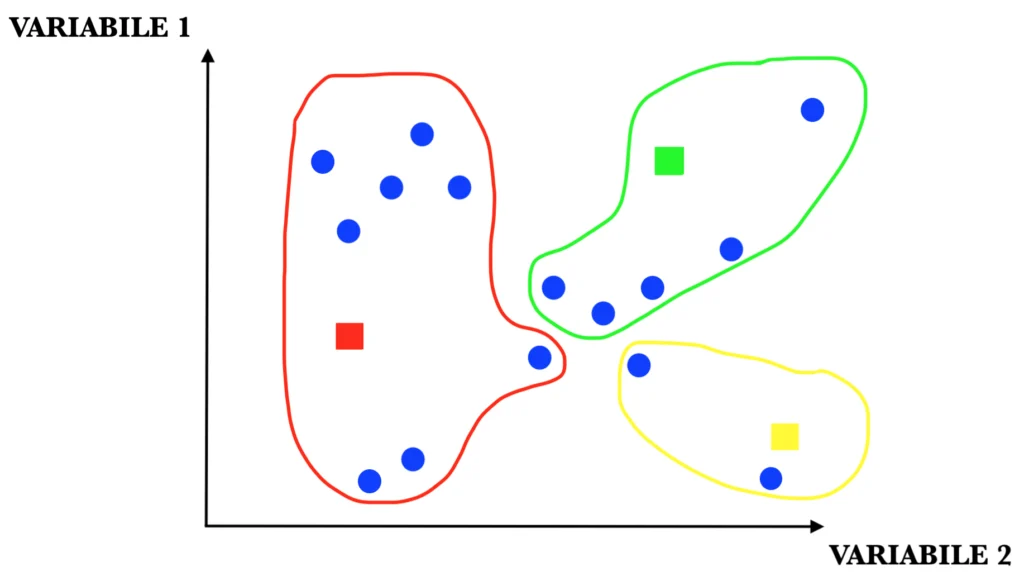
STEP 3: ricalcolo dei centroidi. Una volta inizializzati, i centroidi sono riposizionati ad ogni iterazione della proceduranel punto dello spazio che individua la media aritmetica delle distanze tra tutte le coppie di elementi appartenenti al cluster stesso.
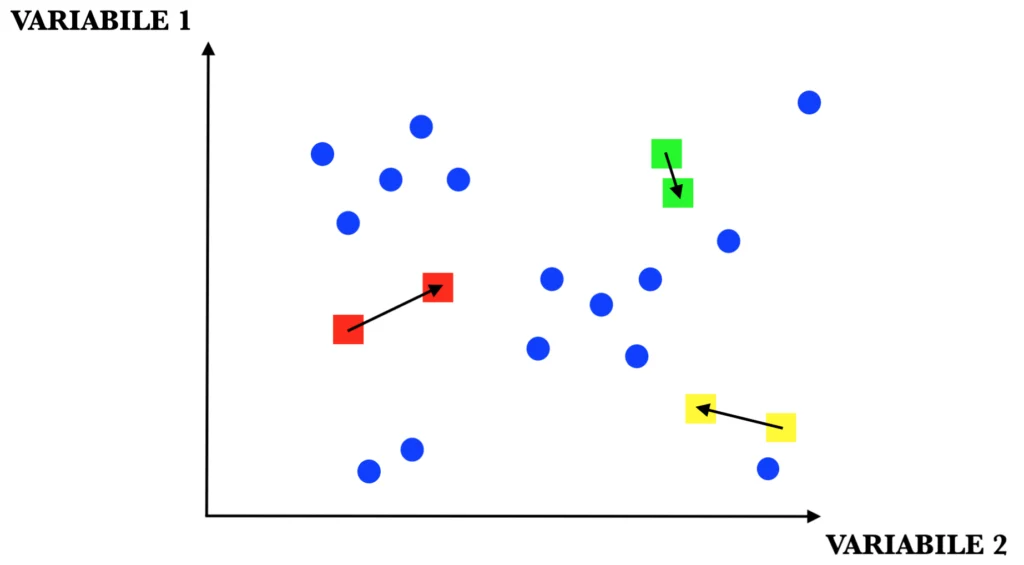
STEP 4: una volta ricostituiti i cluster, se nessun elemento ha cambiato gruppo (si noti l’elemento con la stellina nell’immagine) l’algoritmo termina, altrimenti si riprende dal terzo step.
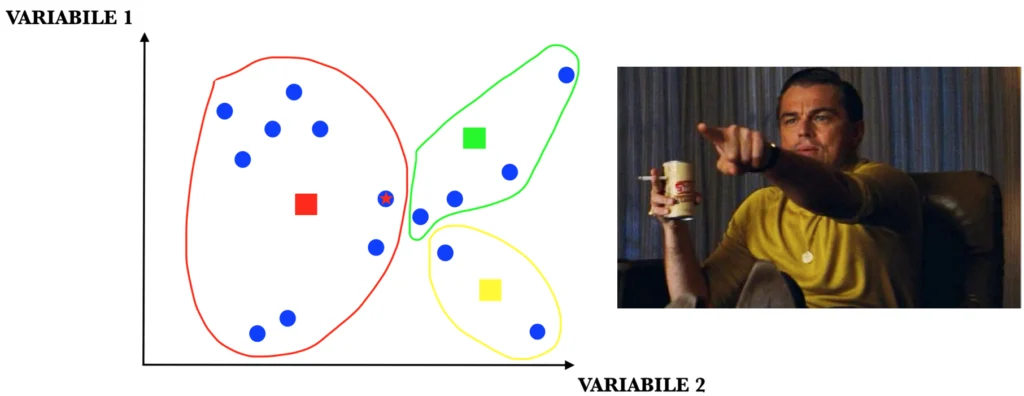
Nelle immagini appena riportate, i puntini blu non sono altro che le 15 persone della tabella iniziale, mentre i quadratinisono i centroidi.
Come si può vedere dalle immagini quindi, tramite l’algoritmo K-Means è stato possibile suddividere i record del dataset, in questo caso costituito da un insieme di persone con caratteristiche differenti, in cluster di elementi tra loro simili. Se la procedura è andata a buon fine, verosimilmente Piergiorgio e Salvatore sono stati inseriti in cluster distinti.
Si può notare quindi la natura non supervisionata degli algoritmi di clustering i quali, non potendo sfruttare alcuna nozione a priori sull’appartenenza di ciascun record ad uno specifico gruppo (in quanto non dispongono di un’etichettache assegni i record ad uno specifico cluster), estraggono questa informazione grazie alla procedura iterativa sopra descritta.
Se quindi un modello supervisionato (come ad esempio una semplice rete neurale) “esprime un giudizio” circa il valore di una variabile etichetta (in questo caso, ad esempio, una rete neurale sarebbe potuta essere utilizzata per imparare, sulla base delle variabili presenti nella tabella, a distinguere se una determinata persona fosse o meno residente nel nord Italia) un modello non supervisionato crea nuove informazioni riguardanti i dati, etichettandoli come appartenenti ad un determinato gruppo.
Una domanda che potrebbe sorgere ad un lettore particolarmente attento è la seguente: com’è stato possibile, nelle immagini sopra, visualizzare in un diagramma a due dimensioni (chiamate volutamente in modo generico variabile 1 e variabile 2) lo spazio a 9 dimensioni descritto nella tabella? A cosa si riferiscono le due variabili “variabile 1” e “variabile 2”?
La risposta a questa domanda non è affatto banale; analizzeremo la soluzione a questo problema in un prossimo articolo dedicato alla temibile PCA, acronimo che sta per “Principal Component Analysis”.
Francesco
